RANGO Y DOMINIO DE UNA FUNCION

Funciones.

Relaciones y Funciones. 

Para saber lo que vamos hacer primero debemos saber los conceptos básicos

Conceptos Básicos.

Relación: Correspondencia o conexión que hay entre dos o mas cosas.

Función: Es una relación de correspondencia, entre un conjunto de datos (x) y otro conjunto de elementos llamado (y); de forma de que cada elemento (x) le corresponde un único elemento del condominio.

Rango: Es el conjunto formado por los valores que pueden llegar a formar la función.

Dominio: es el conjunto de existencia de la función misma, es decir, los valores para cuales la función esta definida.

Entonces entendemos que las funciones matemáticas, en términos simples,  

corresponden al proceso lógico común que se expresa como “depende de”. 

Este proceso lógico se aplica a todo lo que tiene relación a un resultado oefecto

sea este medible o no en forma cuantitativa. 

Ejemplos: 

¿Cuál sería la regla que relaciona los números de la

Derecha con los de la izquierda en la siguiente lista?: 

1 --------> 1

2 --------> 4 

3 --------> 9 

4 --------> 16

Los números de la derecha son los cuadrados de los de la izquierda. La regla es entonces "elevar al cuadrado": 

x -------> x².

Para referirse a esta regla podemos usar un nombre, que por lo general es la letra 

f (de función). f es la regla "elevar al cuadrado el número". Usualmente se emplean dos notaciones:

x --------> x² ó f(x) = x²

La función se gráfica de la siguiente manera

x	Y
-3	-9
-2	-4
-1	-1
0	0
1	1
2	4
3	9

Donde la tabla de la derecha representa los valores de (x) y (y) cuando la función es f(x)=X²

Rango y Dominio

El dominio de la función  f(x)=X² seria (-∞,∞)

El Rango de la función seria  f(x)=X² seria [0,∞)

*El Dominio es todos los valores que ocupa la función en "x" y el Rango todos los 

Valores que ocupa la funciona en "y".

Ejemplo 1:

En esta función f(x) = x³

El Dominio seria (-∞,∞)

El Rango seria  (-∞,∞)

Ejemplo 2:

En esta función f(x) = x - 1 / x² - x - 6

 El Dominio seria (-∞,-2) μ (-2,3) μ (3, ∞)

El Rango seria  (-∞, ∞)

Ejemplo 3:

En esta función f(x)=√x+3

El Dominio seria (-3,∞)

El Rango seria  (0,∞)

Tipos De Funciones

1.- Algebraicas:

Las Funciones algebraicas satisfacen una ecuacion polinomica, cuyos coeficientes son 

polinomios o monomios.

En ellas podemos encontrar:

Funciones Polinomiales: Una función polinomial del grado n es una función de la 

forma : 

Las características globales de una función polinómica son:

a) El dominio es lR

b) No tienen asíntotas.

c) El número de cortes con el eje OX es como máximo el grado del polinomio, y los cortes son las raíces reales del polinomio.

d) El término independiente del polinomio es el que indica el corte con el eje OY.

Ejemplo: 

El Dominio seria (-∞,∞)

El Rango seria  (-∞,∞)

Funciones Racionales:Las funciones racionales están definidas o tienen sudominio de definición en todos los valores de x que no anulen el denominador. Siempre se relacionan con un cociente.

Una función racional es una función que puede ser expresada de la forma: 

a) El dominio de definición son todos los números reales menos las raíces del denominador.

b) Son discontinuas en los valores de x que son las raíces del denominador.

c) Tienen asíntotas verticales en cada raíz del denominador que no lo sea del numerador.

d) Tiene asíntotas horizontales si el grado del numerador es menor o igual que el denominador.

e) Tiene asíntotas oblicuas si el grado del numerador es uno más que el del denominador.

Ejemplo: 

El Dominio seria(-∞,-2) μ(-2,2) μ(2,∞)

El Rango seria  (-∞,o]μ[1.2,∞)

  

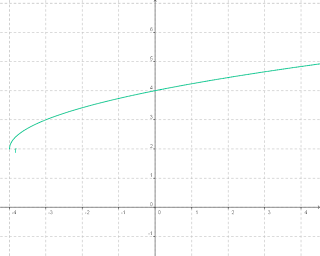
Funciones Irracionales:

Una función es irracional si la variable independiente está bajo el signo del radical.

Ejemplo:

Las características generales de estas funciones son:

a) Si el índice del radical es par, el dominio son los valores para los que el radicando es mayor o igual que cero.

b) Si el índice del radical es impar, el dominio es lR.

c) El recorrido es [0,

∞]

d) Es continua en su dominio y no tiene asíntotas.

El Dominio seria (-4,∞)

 El Rango seria  (2,∞)

2.- Trascendentes: 

Una función trascendente es una función que no satisface una ecuación polinomial cuyos coeficientes sean a su vez polinomios; ésto contrasta con las funciones algebraicas, las cuales satisfacen dicha ecuación. En otras palabras, una función trascendente es una función que trasciende al álgebra en el sentido que no puede ser expresada en términos de una secuencia infinita de operaciones algebraicas de suma, resta y extracción de raíces. 

En Ellas podemos encontrar:

Función Seno: 

La función Seno se obtiene de dividir el cateto opuesto de un triángulo rectángulo, entre su hipotenusa:el seno es la función obtenida al hacer variar la razón mencionada, siendo una de las funciones trascendentes.

Ejemplo: f(x)=sen(x+3)

El Dominio seria (-∞,∞)

El Rango seria  (-1,1)

Funcion Coseno:

La función Coseno se obtiene de dividir el cateto adyacente de un triángulo rectángulo, entre su hipotenusa:

el coseno es la función que asocia un número real x con el valor del coseno del ángulo de amplitud, expresada en radianes, x. 

Ejemplo: f(x)= cos(x²-1)

 

Dominio seria(-∞,∞)

El Rango seria  (-1,1)

Función Tangente: 

La función Tangente se obtiene de dividir el cateto opuesto de un triángulo rectángulo, entre el cateto adyacente:

Se define como la razón entre el cateto opuesto y el adyacente 

O también como la relación entre el seno y el coseno.

Ejemplo:  f(x)= tan x

3.- Logarítmicas:

Las funciones logarítmicas son funciones del tipo f(x)= lognx, donde a (la base) es un número real mayor que cero y distinto de 1.

Tiene las siguientes características generales:

a) El dominio será todos los valores que hacen positivo la expresión dentro del logaritmo.

b) El recorrido es lR.

c) Siempre pasa por el punto (0,1).

d) Siempre pasa por el punto (1,a).

e) Si a>1 la función es creciente.

f) Si 0<a<1 la función es decreciente.

Ejemplo: f(x)= ln(x-1)

El Dominio seria

(1, ∞)

El Rango seria  (-∞, ∞)

4.- Exponenciales.

Las funciones exponenciales son funciones de la forma y=aX, donde a es un número real positivo y distinto de 1.

Las características generales de esta función son:

a) El dominio es lR.

b) Su recorrido es (0, ∞)

c) La función SIEMPRE pasa por el punto (0,1).

d) La función SIEMPRE pasa por el punto (1.a)

e) Si a>0, la función es creciente.

f) Si 0<a<1, la función es decreciente.

Ejemplo: f(x)= e

El Dominio seria (-∞,∞)

 El Rango seria  (o,∞)